Purpose: To demonstrate that the Impulse Momentum theorem is true, by simulating an elastic and inelastic collisions.
Theory: Impulse is equal to the force of the cart integrated with respect to time, on a graph this can be presented as the area underneath a line on a force vs. time graph. Impulse is also determined by the change in momentum (Pf-Pi), so if we set an apparatus to measure the force of an elastic collision over time, and measure the change in velocity after the collision (P=Mass*Velocity) and compare the two, they should be the same. For an inelastic collision
Procedure:
*Experiment 1: Set up an apparatus of a track, a cart with a force gage on the front and a rubber stopper attached to the gage, a velocity sensor pointing down the track, and another cart fastened to the table with a spring to simulate an elastic collision for the rubber stopper to bounce off of during the collision. Determine mass of the cart. Push the cart so it moves towards the cart with the spring, after the collision, integrate the force graph with respect to time, and find the velocity of the moving cart before and after the collision. Calculate the change in momentum and compare it to the Impulse determined by the integration of the force graph.
*Experiment 2: Repeat Experiment 1 with extra mass added to the moving cart, and note any differences from the results.
*Experiment 3: Replace the cart with the spring with a wood block with clay attached to it, add a nail to the moving cart so it will stick to the clay on collision. Note any difference in impulse determined by integration and change in momentum in comparison to the previous experiments.
Apparatus
Experiment 1
Graph Force vs Time and Velocity vs Time
*The area of the force shape and the horizontal axis (the integral) is 0.8923
*Mass of the cart 0.727 kg
*Velocity before collision -0.61 m/s
*Velocity after collision 0.6019 m/s
*The calculation:
Impulse= Mass*Velocity_After - Mass* Velocity_Before
Impulse= (0.727)*(0.6019)-(0.727)*(-0.61)
Impulse= 0.4376+4435
Impulse= 0.8810 kg*m/s
*The calculated Impulse and the Impulse determined from the force graph ((0.8923-0.8810)/0.8923 * 100%) have only a 1.1% percent error between the two.
Experiment 2
*We added 0.3 kg to the moving cart
Graph
*The area of the force shape and the horizontal axis (the integral) is 0.8530
*Mass of the cart 1.027 kg
*Velocity before collision -0.4680 m/s
*Velocity after collision 0.385 m/s
*Calculation was done as before and Impulse determined to be 0.876031 kg*m/s
* 2.7% difference from impulse of force graph.
Experiment 3
*This will be an inelastic collision due to the nail and clay on the cart and wood block replacing the spring cart
*The area of the force shape and the horizontal axis (the integral) is 0.2715
*Mass of the cart 1.027 kg
*Velocity before collision -0.2647 m/s
*Velocity after collision 0 m/s
*Calculation was done as before and Impulse determined to be 0.2718 kg*m/s
* 0.13 % difference from impulse of force graph.
Conclusion
*The difference between the calculated impulse and determined impulse was minute, so the Impulse momentum theorem seems confirmed.
*The inelastic was a sharp spike that was a smaller value than the elastic collisions, I understand mathematically why this is the case (a zero value for the final velocity resulted in only the initial velocity being considered in determining Impulse), but not fully understanding conceptually why this is. Perhaps because the force that would have "pushed back" on the cart was "lost" into the greater system of the block, the table, and the rest of the Earth.
*Sources of error for the experiment are, it doesn't take into account friction between the cart and track or from air resistance.
Thursday, April 23, 2015
13-April-2015 Magnetic Potential Energy
Purpose: To create an expression for potential energy from a two same charged magnets (U_mag) using what we know of kinetic energy (KE) and the forces involved on an air track.
Theory: Because energy is conserved within a system, the kinetic energy of a moving cart on an air track should transfer to the potential energy created by the magnets (assuming no other energy is added or removed from the system), the relationship graphed should look something like this over time.
Procedure: Set up an air track with a magnet on one end, with a cart with another magnet on it. Weigh the cart for its mass, once its on the track incline the track at various steeper angles and measure the distance between the magnets, make a free body diagram of the forces on the cart, graph these points and find a line that expresses this Force vs distance between magnets. The expression for the line once integrated with regards to distance between the magnets and multiplied by negative one is our model for U_mag, we test the accuracy of this model by moving the cart along the track (creating KE with out too much friction), and seeing if the energy is conserved or not (since it must for our model to be accurate).
Apparatus
Forces on the Cart
*So the force of the magnets is Mass of cart * gravity * the sine of the angle the track makes with the horizontal.
*We measured the distance between the magnets at varying angles.
*Mass of the cart was weighed to be 0.34 kg.
Results
Graph of Force vs Distance
*The best fit line is A*y^B.
*A is a constant and = 0.0001316
*B is the power value of the line and is = -1.956
*y is the distance between the magnets and is the value we integrate with respect to (dy).
* Once integrated our model for (limits of integration 0 to y) and multiplied by negative one is
U_mag= -Int(0.0001316*y^-1.956 dy) from 0 to y
U_mag= -0.0001316/(-1.956+1) (y^-1.956+1.0)
U_mag= (-0.0001316/-0.956)*y^-0.956
U_mag=0.000137657*y^--0.956
*We now test this model with the KE (0.5*Mass of cart*Velocity^2) of the cart as it approaches the magnet, the position sensor records the distance between the magnets, and we graph the results.
Graph KE and U_mag vs time
*Are graph isn't ideal; although there is an inverse relationship between KE and U_mag, they aren't equal, suggesting that something was contributing to the KE as it approached the magnets.
*The slant from the KE line suggests the track was at an angle, potential energy from gravity was effecting the system on its way towards and away from the magnets.
Conclusion
*Although I still believe the methods were valid, too much human error caused unsatisfactory results.
*Our final graph has an obvious slant, meaning the track wasn't level and energy due to gravity effected the results.
*The experiment ignores friction caused by the air against the cart, though because of the nature of an air track there was no friction between the cart and the track.
*We relied on the human eye and a ruler to measure the distance between the magnets in the first part of the lab, meaning our results could there could only be accurate up to +/- 0.0005 meters, though the U_mag that was derived from those results behaved as expected.
Theory: Because energy is conserved within a system, the kinetic energy of a moving cart on an air track should transfer to the potential energy created by the magnets (assuming no other energy is added or removed from the system), the relationship graphed should look something like this over time.
Procedure: Set up an air track with a magnet on one end, with a cart with another magnet on it. Weigh the cart for its mass, once its on the track incline the track at various steeper angles and measure the distance between the magnets, make a free body diagram of the forces on the cart, graph these points and find a line that expresses this Force vs distance between magnets. The expression for the line once integrated with regards to distance between the magnets and multiplied by negative one is our model for U_mag, we test the accuracy of this model by moving the cart along the track (creating KE with out too much friction), and seeing if the energy is conserved or not (since it must for our model to be accurate).
Apparatus
Forces on the Cart
*So the force of the magnets is Mass of cart * gravity * the sine of the angle the track makes with the horizontal.
*We measured the distance between the magnets at varying angles.
*Mass of the cart was weighed to be 0.34 kg.
Results
Angle (Rad)
|
Force Magnets (N)
|
Distance (M)
|
0.06108472
|
0.203407742
|
0.023
|
0.09075444
|
0.301978875
|
0.02
|
0.11693361
|
0.388735483
|
0.017
|
0.14485806
|
0.480980775
|
0.015
|
0.1727825
|
0.572851035
|
0.014
|
0.26877278
|
0.884807519
|
0.011
|
Graph of Force vs Distance
*The best fit line is A*y^B.
*A is a constant and = 0.0001316
*B is the power value of the line and is = -1.956
*y is the distance between the magnets and is the value we integrate with respect to (dy).
* Once integrated our model for (limits of integration 0 to y) and multiplied by negative one is
U_mag= -Int(0.0001316*y^-1.956 dy) from 0 to y
U_mag= -0.0001316/(-1.956+1) (y^-1.956+1.0)
U_mag= (-0.0001316/-0.956)*y^-0.956
U_mag=0.000137657*y^--0.956
*We now test this model with the KE (0.5*Mass of cart*Velocity^2) of the cart as it approaches the magnet, the position sensor records the distance between the magnets, and we graph the results.
Graph KE and U_mag vs time
*Are graph isn't ideal; although there is an inverse relationship between KE and U_mag, they aren't equal, suggesting that something was contributing to the KE as it approached the magnets.
*The slant from the KE line suggests the track was at an angle, potential energy from gravity was effecting the system on its way towards and away from the magnets.
Conclusion
*Although I still believe the methods were valid, too much human error caused unsatisfactory results.
*Our final graph has an obvious slant, meaning the track wasn't level and energy due to gravity effected the results.
*The experiment ignores friction caused by the air against the cart, though because of the nature of an air track there was no friction between the cart and the track.
*We relied on the human eye and a ruler to measure the distance between the magnets in the first part of the lab, meaning our results could there could only be accurate up to +/- 0.0005 meters, though the U_mag that was derived from those results behaved as expected.
8-April-15 Conservation of Energy-Mass Spring System
Purpose: To show that the energy of an oscillating spring's, with a hanging mass in the vertical position, energy will be conserved during the oscillation in both the attached mass and the spring.
Theory: Since energy is conserved, the graphs can represent the relationship between the potential energy (elastic from the spring and gravitational on both the spring and hanging mass) and kinetic energy (of both the spring and the mass) in a manner that makes sense from what we know of the initial energy of a system must equaling the finial energy of a system.
Procedure: We determine the mass of our spring, we set up our apparatus to hang a spring off of (attached to a force gage) and a position sensor on the floor. Determine the K constant of our spring (we will need this for when we determine the elastic potential energy (EPE)) by attaching a mass to stretch the string and measure the resulting force and stretch. Derive an expression for the kinetic energy of the spring and potential energy due to gravity on the spring. Stretch the spring, with the mass attached, and allow it to oscillate at a nice steady rate. Graph results and compare.
Apparatus
*We weighed our spring to have a mass of 0.121 kg
*We attached a heavy enough mass to stretch the string, and graphed the resulting force vs. stretch
*The slope is our K constant for the spring 18.79 N/M.
*We know EPE is determined by 0.5*K*(stretch)^2, so we make a column that will determine this for us by imputing the stretch during the oscillation
*For the hanging mass we already have expressions to calculate energy (KE=0.5*Mass*Velocity^2, GPE=Mass*gravity*height).
*We calculate the KE and GPE for the spring by taking a representative piece and rewriting it in terms of dy (dm/dy = Mass/(Height- y end of spring), limits of integration y end to Height, GPE then should be = dm*g*y.
*Fully calculated GPE_spring= Mass_spring*gravity*(Height -y end)*0.5, and Height - yend is merely the position read by the position sensor.
*We calculate the KE of the spring by once again rewriting everything in terms of dy(dm/Mass = dy/Length of spring), limits of integration 0 to Length, KE then should be = 0.5*dm* y/L*velocity. (velocity of the piece is equal to y/Length * velocity of the mass)
*Fully calculated KE_spring = 1/6 * Mass_spring * Velocity^2
*We can now add a 0.2 kg mass to the spring (hanging mass), and begin oscillating
Graphs
GPE_spring, KE_mass, and KE_spring
*We see that when the GPE_spring is at its max, both the KE_spring and KE_mass are at zero
*This makes sense as GPE_spring's max energy is when the system is at its highest point and about to fall, meaning the velocity is zero as their is no motion yet. If the velocity is zero, both KE of the spring and mass must also be zero.
EPE and GPE_mass
*We again see graphs that are mirror opposites of each other.
*This again makes sense as the EPE is at its max when the spring is stretched to its max, this point's position however is considered the zero mark of our height, therefore the GPE_mass is zero as well.
GPE_mass, GPE_spring, KE_mass, KE_spring, EPE, Sum of all Energy vs time
*In general we do see the sum of energy remaining the same throughout the oscillations, returning to the previous peaks and valleys over time, as well as all the other energy graphs
*Although not very apparent, we do see smaller peaks and valleys of the graphs over time.
*This makes sense as energy is being lost during each oscillation due to friction from the air.
GPE_mass, GPE_spring, KE_mass, KE_spring, EPE, Sum of all Energy vs position
*We see some very straight(ish) lines from the sum of forces
*Straight lines would make sense as the energy is never really being lost throughout the process, meaning the energy is conserved.
*I believe the reasoning for any "slants" within the sum is due to a scaling the graphs.
Conclusion
*All around the graphs behaved consistently with what I would expect if the conservation of energy is true.
*Any "leveling off" of the graphs can be explained as due to air friction doing work against the system, stealing energy.
*There was some inconstancy with the Sum of energy vs position graph, as it seems to gain energy over time, but I believe that was due to me not properly scaling the graph
Theory: Since energy is conserved, the graphs can represent the relationship between the potential energy (elastic from the spring and gravitational on both the spring and hanging mass) and kinetic energy (of both the spring and the mass) in a manner that makes sense from what we know of the initial energy of a system must equaling the finial energy of a system.
Procedure: We determine the mass of our spring, we set up our apparatus to hang a spring off of (attached to a force gage) and a position sensor on the floor. Determine the K constant of our spring (we will need this for when we determine the elastic potential energy (EPE)) by attaching a mass to stretch the string and measure the resulting force and stretch. Derive an expression for the kinetic energy of the spring and potential energy due to gravity on the spring. Stretch the spring, with the mass attached, and allow it to oscillate at a nice steady rate. Graph results and compare.
Apparatus
*We weighed our spring to have a mass of 0.121 kg
*We attached a heavy enough mass to stretch the string, and graphed the resulting force vs. stretch
*The slope is our K constant for the spring 18.79 N/M.
*We know EPE is determined by 0.5*K*(stretch)^2, so we make a column that will determine this for us by imputing the stretch during the oscillation
*For the hanging mass we already have expressions to calculate energy (KE=0.5*Mass*Velocity^2, GPE=Mass*gravity*height).
*We calculate the KE and GPE for the spring by taking a representative piece and rewriting it in terms of dy (dm/dy = Mass/(Height- y end of spring), limits of integration y end to Height, GPE then should be = dm*g*y.
*Fully calculated GPE_spring= Mass_spring*gravity*(Height -y end)*0.5, and Height - yend is merely the position read by the position sensor.
*We calculate the KE of the spring by once again rewriting everything in terms of dy(dm/Mass = dy/Length of spring), limits of integration 0 to Length, KE then should be = 0.5*dm* y/L*velocity. (velocity of the piece is equal to y/Length * velocity of the mass)
*Fully calculated KE_spring = 1/6 * Mass_spring * Velocity^2
*We can now add a 0.2 kg mass to the spring (hanging mass), and begin oscillating
Graphs
GPE_spring, KE_mass, and KE_spring
*We see that when the GPE_spring is at its max, both the KE_spring and KE_mass are at zero
*This makes sense as GPE_spring's max energy is when the system is at its highest point and about to fall, meaning the velocity is zero as their is no motion yet. If the velocity is zero, both KE of the spring and mass must also be zero.
EPE and GPE_mass
*We again see graphs that are mirror opposites of each other.
*This again makes sense as the EPE is at its max when the spring is stretched to its max, this point's position however is considered the zero mark of our height, therefore the GPE_mass is zero as well.
GPE_mass, GPE_spring, KE_mass, KE_spring, EPE, Sum of all Energy vs time
*In general we do see the sum of energy remaining the same throughout the oscillations, returning to the previous peaks and valleys over time, as well as all the other energy graphs
*Although not very apparent, we do see smaller peaks and valleys of the graphs over time.
*This makes sense as energy is being lost during each oscillation due to friction from the air.
GPE_mass, GPE_spring, KE_mass, KE_spring, EPE, Sum of all Energy vs position
*We see some very straight(ish) lines from the sum of forces
*Straight lines would make sense as the energy is never really being lost throughout the process, meaning the energy is conserved.
*I believe the reasoning for any "slants" within the sum is due to a scaling the graphs.
Conclusion
*All around the graphs behaved consistently with what I would expect if the conservation of energy is true.
*Any "leveling off" of the graphs can be explained as due to air friction doing work against the system, stealing energy.
*There was some inconstancy with the Sum of energy vs position graph, as it seems to gain energy over time, but I believe that was due to me not properly scaling the graph
Friday, April 10, 2015
6-April-2015 Work-Kinetic Energy Therom
Purpose: To show that work and kinetic energy are both measured in joules, and therefore are really the "same thing," as the energy is being transferred from motion into a spring.
Theory: That near all the energy of a stretched string is transferred to a cart to make it move, so the stored energy is transferred to give the cart kinetic energy, and this amount of energy can be determined by the area underneath a graph of Force vs position.
Procedure: Set up a track and attach a spring to a cart and force gage, and use logger pro and a motion sensor to measure the resulting force, position, and velocity from the cart because of the spring.
Eperiment 1: Graph the results and determine a K constant for the spring from a Force vs. Position data by stretching out the string.
Experiment 2: Determine the mass of the cart, set up another experiment to measure the velocity of the cart after the spring is released and set up a new graph that is "laid on top of" a Force vs. Position graph of the spring, but create a calculated column for the y-axis to measure the kinetic energy of the cart, so that it is a Kinetic Energy vs Position graph and determine if there is correlation between the two graphs.
Experiment 3: Watch a short video, determine the area under the graph in the video to find the total energy stored in a rubber band, the stored energy is then transferred to a cart, and with the given mass distance and time calculate the kinetic energy and compare it to the expected amount determined form the graph.
The System
Experiment 1
*For Experiment 1 this is the graph we got.
*The energy on a Force vs Position graph can be determined by the area underneath the line formed.
*Because the line is nearly perfectly straight, the graph is similar to a triangle.
*The area underneath a triangle 1/2 * Base*Height, and in this triangle the base is position (x) and the height is the force.
*The energy from a spring is 1/2 *Spring Constant(K)*x^2, so setting that equal to the area and solving for K should give us the spring constant.
*Because of issues calibrating, area had to be solved by hand.
*Base= 0.21 m
*Height=0.63 N
*Area=0.06615 J
*Area=1/2 *K* x^2 (x is equal to base)
*K=3 N/m
Experiment 2
*The same set up was used, though the calibration errors were fixed.
*Mass of cart was determined to be 0.539 kg.
*By measuring the velocity as the cart is pulled, the kinetic energy of the cart could be determined as it was pulled by the spring.
*Creating another graph with this calculation as the y-axis creates a Kinetic energy vs Position graph, and means that any y-point on the that graph should be equal to the area under the Force vs Position graph at the same x-point.
Graphs
*Kinetic energy equals 0.064 J, area under Force vs Position graph =0.06108
*Kinetic energy equals 0.107 J, area under Force vs Position graph =0.1073
*Kinetic energy equals 0.125 J, area under Force vs Position graph =0.1315
Experiment 3
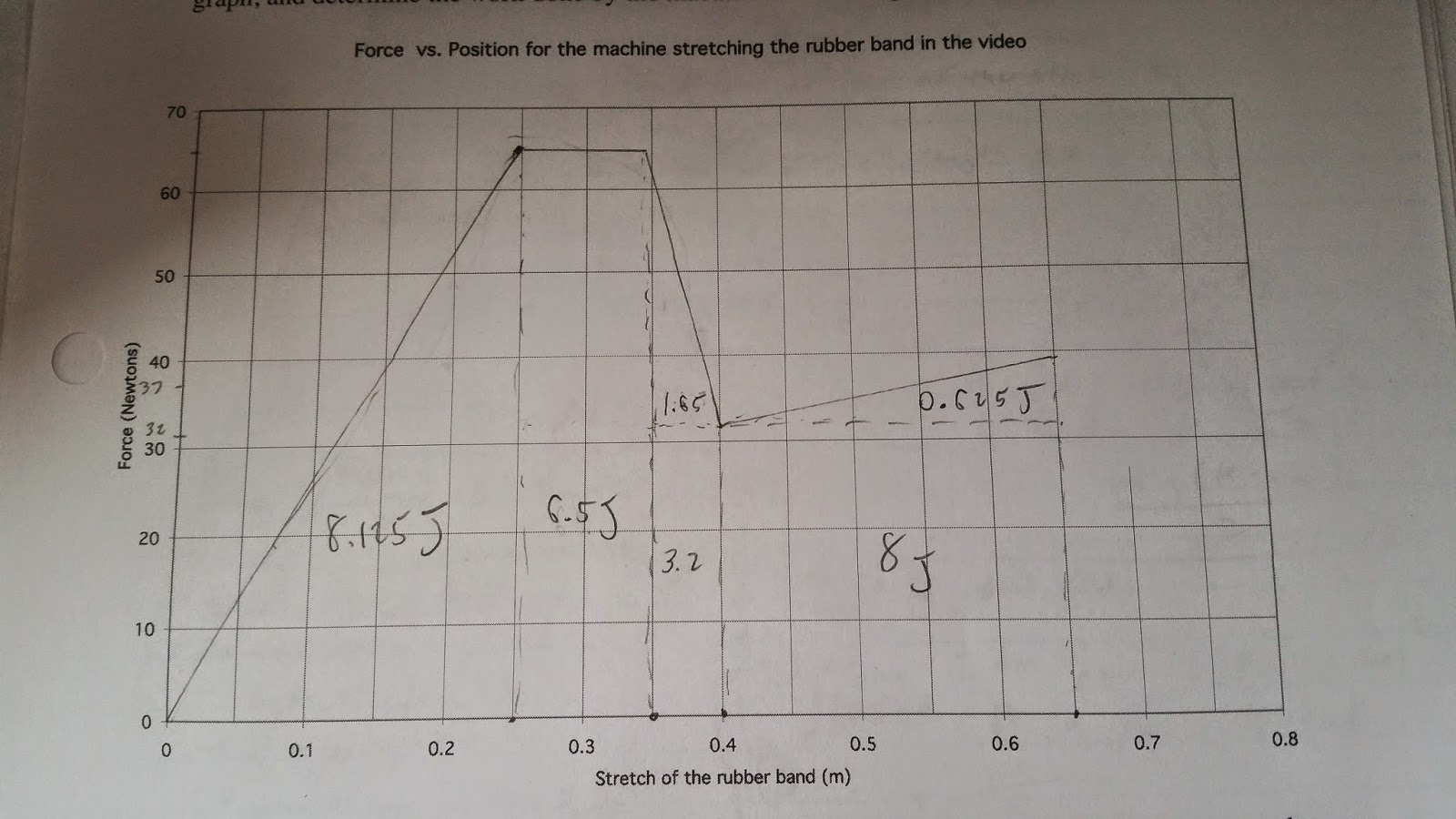
*The Graph from the video was traced, and the are underneath was broken up into six simple shapes for calculating area (three rectangles and three triangles)
Graph
*Triangle_1=8.125 J, Triangle_2=0.825 J, and Triangle_3= 0.625 J
*Rectangle_1= 6.5 J, Rectangle_2= 1.6 J, and Rectangle_3= 8 J
*Total area= 25.675 J
*At the end of the video we were given a set distance a cart (mass= 4.3 kg) would travel (0.15 m) in 0.045 seconds from the amount of energy from the area of the above graph transferred to it.
*Since kinetic energy equals 1/2 *mass*velocity^2, the two values should be equal.
*Calculated energy = 1/2 *4.3 *(0.15/0.045)^2 = 23.89 J
Conclusion
*In Experiment 2 the calculated Kinetic energy and the area under the Force vs position graph for the spring were nearly identical (except for the area being a negative number because it was determined through integration). Trial one had 4.5% difference, trial two was exact, and trial three was 5.2 % difference. It seems obvious the energy/work from the spring was transferred to the kinetic energy for the cart.
*Flaws with the system are it doesn't account for friction from the cart and track and from the air.
*In Experiment 3 the difference was around 7.4 % between the calculated energy from how fast the cart moved from the stored energy(Kinetic energy), and the amount determined from the Force vs. Position graph.
*The Force vs. Position graph was fraught with uncertainties, as it was completely determined through "eye-balling" a grainy old time video, and trying to replicate the graph on another paper.
Theory: That near all the energy of a stretched string is transferred to a cart to make it move, so the stored energy is transferred to give the cart kinetic energy, and this amount of energy can be determined by the area underneath a graph of Force vs position.
Procedure: Set up a track and attach a spring to a cart and force gage, and use logger pro and a motion sensor to measure the resulting force, position, and velocity from the cart because of the spring.
Eperiment 1: Graph the results and determine a K constant for the spring from a Force vs. Position data by stretching out the string.
Experiment 2: Determine the mass of the cart, set up another experiment to measure the velocity of the cart after the spring is released and set up a new graph that is "laid on top of" a Force vs. Position graph of the spring, but create a calculated column for the y-axis to measure the kinetic energy of the cart, so that it is a Kinetic Energy vs Position graph and determine if there is correlation between the two graphs.
Experiment 3: Watch a short video, determine the area under the graph in the video to find the total energy stored in a rubber band, the stored energy is then transferred to a cart, and with the given mass distance and time calculate the kinetic energy and compare it to the expected amount determined form the graph.
The System
Experiment 1
*For Experiment 1 this is the graph we got.
*The energy on a Force vs Position graph can be determined by the area underneath the line formed.
*Because the line is nearly perfectly straight, the graph is similar to a triangle.
*The area underneath a triangle 1/2 * Base*Height, and in this triangle the base is position (x) and the height is the force.
*The energy from a spring is 1/2 *Spring Constant(K)*x^2, so setting that equal to the area and solving for K should give us the spring constant.
*Because of issues calibrating, area had to be solved by hand.
*Base= 0.21 m
*Height=0.63 N
*Area=0.06615 J
*Area=1/2 *K* x^2 (x is equal to base)
*K=3 N/m
Experiment 2
*The same set up was used, though the calibration errors were fixed.
*Mass of cart was determined to be 0.539 kg.
*By measuring the velocity as the cart is pulled, the kinetic energy of the cart could be determined as it was pulled by the spring.
*Creating another graph with this calculation as the y-axis creates a Kinetic energy vs Position graph, and means that any y-point on the that graph should be equal to the area under the Force vs Position graph at the same x-point.
Graphs
*Kinetic energy equals 0.064 J, area under Force vs Position graph =0.06108
*Kinetic energy equals 0.107 J, area under Force vs Position graph =0.1073
*Kinetic energy equals 0.125 J, area under Force vs Position graph =0.1315
Experiment 3
*The Graph from the video was traced, and the are underneath was broken up into six simple shapes for calculating area (three rectangles and three triangles)
Graph
*Triangle_1=8.125 J, Triangle_2=0.825 J, and Triangle_3= 0.625 J
*Rectangle_1= 6.5 J, Rectangle_2= 1.6 J, and Rectangle_3= 8 J
*Total area= 25.675 J
*At the end of the video we were given a set distance a cart (mass= 4.3 kg) would travel (0.15 m) in 0.045 seconds from the amount of energy from the area of the above graph transferred to it.
*Since kinetic energy equals 1/2 *mass*velocity^2, the two values should be equal.
*Calculated energy = 1/2 *4.3 *(0.15/0.045)^2 = 23.89 J
Conclusion
*In Experiment 2 the calculated Kinetic energy and the area under the Force vs position graph for the spring were nearly identical (except for the area being a negative number because it was determined through integration). Trial one had 4.5% difference, trial two was exact, and trial three was 5.2 % difference. It seems obvious the energy/work from the spring was transferred to the kinetic energy for the cart.
*Flaws with the system are it doesn't account for friction from the cart and track and from the air.
*In Experiment 3 the difference was around 7.4 % between the calculated energy from how fast the cart moved from the stored energy(Kinetic energy), and the amount determined from the Force vs. Position graph.
*The Force vs. Position graph was fraught with uncertainties, as it was completely determined through "eye-balling" a grainy old time video, and trying to replicate the graph on another paper.
1-April-2015 Centripetal force with a motor
Purpose: To show mathematically (through the slope of a chart) that as the apparatus spins, thus increasing its centripetal acceleration, the omega (rotations per second converted to radians per second) increases, and so to will the angle the tether makes with the vertical axis.
Theory: As the centripetal acceleration increases on a mass tethered to the apparatus, so to will the angle made between the tether and vertical axis. The omega (w), which will be determined separately, can be expressed using that angle and measurements of the apparatus and forces on the mass. The expression should equal the w that was determined separately, and so the chart of w vs. the expression should make a straight line with 1/1 slope.
Procedure: Measure the height (H) of the apparatus, the Length of the tether (L), the distance between the mass and center of the apparatus at rest (R). Have the apparatus spin at differing speeds six separate times, timing how long it takes to complete ten rotations for each spin speed, and measure the height the mass makes with the ground during each of the spin speeds (h). Calculate w, and then find an expression for w using the measurements taken, using known formulas.
*The Apparatus
*H is measured to be 2 meters +/- 0.0005 meters
*L is measured to be 1.66 meters +/- 0.001 meters
*R is measured to be 0.96 meters +/- 0.0005 meters
*w is calculated by taking the 10 revolutions dividing by the time and multiplied by 2Pi of each spin speed.
*h will vary at different spin speeds.
* The angle L makes with the vertical axis at any spin speed can be determined by realizing a 90 degree triangle is made during each spin speed.
* The angle at each spin speed is than (arc cos ((H-h)/L))
*Additionally the distance of the mass from the center of the apparatus will be (R+L sin (angle))
* The forces on the mass.
*T can be found to be mg/cos (angle), and so a_c=g*Tan (angle) with the mass canceled out.
*Centripetal acceleration (a_c) is equal to radius*w^2
* The radius was determined to be the distance= (R+L sin angle)
*Plugging all three equations into one another, and solving for w, gives us the expression
(w=Sq_root of (g*Tan (angle)/(R+L sin (angle))
Graph of Calculated w (using angle and other measurements) vs actual w
*We get a line that can be expressed as y=0.9455x+0.0661, meaning the slope is 0.9455
Conclusion
* There was only a 5.45% difference between the "actual" value of the expected w.
*Problems with the experiment are, the "actual" values of w were determined using the human eye and a stop watch, error could have come from human error here.
*The measurements did have uncertainty, which could have been accounted for in the actual experiment if I was more certain on how to calculate error beyond using propagated error from partial derivatives.
*Overall I am satisfied with the results, and feel experiment showed through the equations a relation between the angle formed by the centripetal acceleration and omega.
Theory: As the centripetal acceleration increases on a mass tethered to the apparatus, so to will the angle made between the tether and vertical axis. The omega (w), which will be determined separately, can be expressed using that angle and measurements of the apparatus and forces on the mass. The expression should equal the w that was determined separately, and so the chart of w vs. the expression should make a straight line with 1/1 slope.
Procedure: Measure the height (H) of the apparatus, the Length of the tether (L), the distance between the mass and center of the apparatus at rest (R). Have the apparatus spin at differing speeds six separate times, timing how long it takes to complete ten rotations for each spin speed, and measure the height the mass makes with the ground during each of the spin speeds (h). Calculate w, and then find an expression for w using the measurements taken, using known formulas.
*The Apparatus
*H is measured to be 2 meters +/- 0.0005 meters
*L is measured to be 1.66 meters +/- 0.001 meters
*R is measured to be 0.96 meters +/- 0.0005 meters
*w is calculated by taking the 10 revolutions dividing by the time and multiplied by 2Pi of each spin speed.
times
|
Rad/s
|
39.79
|
1.579087
|
33.8
|
1.858931
|
28.7
|
2.189263
|
25.34
|
2.479552
|
21.39
|
2.937441
|
17.71
|
3.547818
|
*h will vary at different spin speeds.
h values (m)
|
0.455
|
0.578
|
0.832
|
1.02
|
1.26
|
1.48
|
* The angle L makes with the vertical axis at any spin speed can be determined by realizing a 90 degree triangle is made during each spin speed.
* The angle at each spin speed is than (arc cos ((H-h)/L))
angle (rad)
|
0.3744118
|
0.5421012
|
0.7903249
|
0.9392897
|
1.1087474
|
1.2521798
|
*Additionally the distance of the mass from the center of the apparatus will be (R+L sin (angle))
radius (m)
|
1.567104
|
1.816455
|
2.139566
|
2.299851
|
2.445934
|
2.536452
|
* The forces on the mass.
*T can be found to be mg/cos (angle), and so a_c=g*Tan (angle) with the mass canceled out.
*Centripetal acceleration (a_c) is equal to radius*w^2
* The radius was determined to be the distance= (R+L sin angle)
*Plugging all three equations into one another, and solving for w, gives us the expression
(w=Sq_root of (g*Tan (angle)/(R+L sin (angle))
Calculated w
|
1.567586033
|
1.80261615
|
2.15074983
|
2.413672734
|
2.836446352
|
3.422460172
|
Graph of Calculated w (using angle and other measurements) vs actual w
*We get a line that can be expressed as y=0.9455x+0.0661, meaning the slope is 0.9455
Conclusion
* There was only a 5.45% difference between the "actual" value of the expected w.
*Problems with the experiment are, the "actual" values of w were determined using the human eye and a stop watch, error could have come from human error here.
*The measurements did have uncertainty, which could have been accounted for in the actual experiment if I was more certain on how to calculate error beyond using propagated error from partial derivatives.
*Overall I am satisfied with the results, and feel experiment showed through the equations a relation between the angle formed by the centripetal acceleration and omega.
Subscribe to:
Comments (Atom)